| Voltar |
Este também é um fenômeno que causa muita confusão. Os livros didáticos têm uma explicação quase idêntica entre si, com os mesmos erros semelhantes em todos eles (Canalle et al 1997). O principal erro é colocar a Lua girando ao redor da Terra no mesmo plano em que esta gira ao redor do Sol (Fig.22). Ao se fazer isto causa-se obrigatoriamente 2 eclipses por mês lunar (ou mês sinódico[1]), sendo um eclipse lunar e outro solar. Uma figura típica encontrada nos livros didáticos está esquematizada na Fig. 22.

 Fig. 22 - Típica figura encontrada em livros
didáticos para explicar as fases da Lua.
Fig. 22 - Típica figura encontrada em livros
didáticos para explicar as fases da Lua.
Depreende-se do que está esquematizado na Fig. 22 que toda vez que a Lua estiver na posição 1 haverá eclipse solar e toda vez que passar pela posição 3 haverá eclipse lunar. Como não observamos dois eclipses a cada 29,5 dias, algo deve estar errado com essa figura. Explicaremos os eclipses no próximo item.
A bola de isopor usada nas atividades anteriores, representando a Terra, agora representará a Lua. Sugerimos fixar (espetar) um quadrado de cartolina preta (por exemplo, 5 x 5 cm) sobre a superfície da bola de isopor, próximo ao equador (ou seja, a cartolina ficará tangente a algum ponto próximo ao equador lunar. Este quadrado indicará “São Jorge”, ou seja, a face que está sempre voltada para nós. O esquema utilizado para a explicação, que se segue, das fases da Lua, encontra-se na figura 24.
O Sol continuará sendo representado pela lâmpada, mas substituindo-se o “gorro” de papel alumínio por um tubo de papel alumínio (Fig. 23) para direcionar horizontalmente o feixe de luz sobre a Lua. Para fazer isso a lâmpada será segurada por um aluno (aluno S, fig.24) que apontará seu feixe sempre para a Lua.
![]()
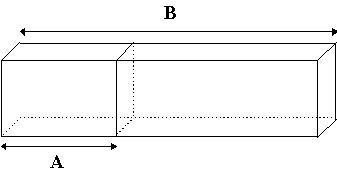
Fig. 23 - No segmento A está representada a embalagem comercial da lâmpada (um paralelogramo sem fundo ou tampa feito de papelão). Ao redor desta embalagem colocamos uma folha de papel alumínio com comprimento de 40 cm formando o tubo de papel alumínio indicado pelo segmento B.
A Terra será representada pela própria cabeça de um aluno (aluno T, fig. 24) que fará as observações. A Lua será carregada ao redor da Terra por outro aluno (aluno L, fig 24), mas de tal forma que o quadrado preto (“São Jorge”) esteja sempre voltado para a Terra. O aluno Terra (T) apenas girará sobre si mesmo sem se transladar.
Com esta montagem sugerimos começar a atividade reproduzindo o erro do livro didático, isto é, faça a Lua girar em torno da Terra num plano paralelo ao chão e passando pelo centro da Terra (cabeça do aluno). Estando o Sol no mesmo plano da Terra e da Lua, quando a Lua estiver na posição 1 da Fig. 22 ou 24 haverá eclipse solar e quando estiver na posição 3 das mesmas Fig.22 ou 24 haverá eclipse lunar. E isso se repetiria a cada mês sinódico. Logo, algo está errado. Como resolver o problema? Existem duas soluções. A primeira é deslocar o plano da órbita da Lua para cima ou para baixo da cabeça do aluno, mas isso é irreal pois o plano da órbita da Lua deve passar pelo centro da Terra. Eliminada esta solução, a outra, que é a correta e evita os dois eclipses mensais, é inclinar o plano da órbita da Lua. Inclinar o plano da órbita da Lua significa que, partindo a Lua da posição 1, quando ela deve estar abaixo da linha definida pela direção Terra-Sol, ela chegará à posição 3 acima do feixe da sombra da cabeça do aluno que representa a Terra (não esquecendo que o plano da órbita da Lua passa pelo centro da Terra). Com isto evita-se os dois eclipses mensais e esta é a situação real, ou seja, a Lua não gira ao redor da Terra no mesmo plano que esta gira ao redor do Sol. A inclinação entre os dois planos é de aproximadamente 5o. Observe, contudo, que os pontos 2 e 4 da Fig. 24 pertencem tanto ao plano da órbita da Lua quanto ao plano a órbita da Terra. Este fato será muito importante quando se estudar os eclipses.
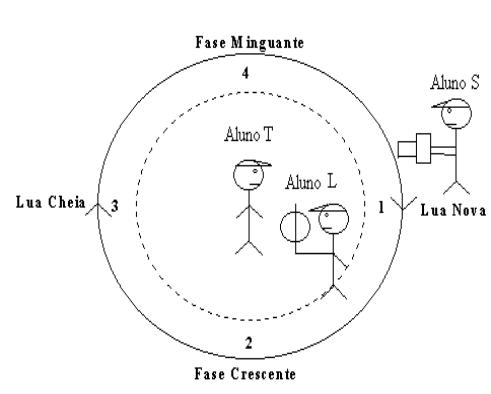
Fig.24 - Esquema do sistema Sol-Terra-Lua. O aluno que segura a lâmpada deve ficar a uns 2 ou 3 metros da Terra, apontando seu feixe de luz sempre para a Lua. O aluno que carrega a Lua deve girar ao redor da Terra a cerca de 1 m ou 1,5 m, mas transladando a Lua num plano tal que na posição 1 a Lua passe abaixo da linha Terra-Sol, nas posições 2 e 4 cruze o plano da órbita da Terra ao redor do Sol, isto é, fica na mesma altura dos olhos do aluno Terra; na posição 3 passe acima da linha Terra-Sol. Obs. No esquema as linhas circulares são vistas de cima e os bonecos representam alunos caminhando sobre o círculo pontilhado e o círculo contínuo foi usado para marcar as fases crescentes, minguantes, cheia e nova.
Quando se evita o problema dos eclipses, define-se simultaneamente a inclinação do plano da órbita da Lua em relação ao plano de órbita da Terra. Na posição 1 a Lua da Fig. 24 está abaixo da linha Terra-Sol; na posição 2 está na mesma altura da cabeça do aluno Terra (seria quando ela estaria cruzando o plano da órbita da Terra), na posição 3 ela está passando acima da linha Terra-Sol; na posição 4 é a mesma situação da posição 2 e recomeça o ciclo na posição 1.
- Lua nova:
É aquela que não se vê, pois ela está na posição 1(abaixo da linha Terra-Sol), logo, o lado voltado para a Terra não está iluminado, além de estarmos olhando na direção do Sol, o qual nos ofusca a visão. Nesta situação dizemos que a Lua nasce junto com o Sol e se põe junto com ele, mas na noite seguinte (o aluno que segura a Lua deve se deslocar cerca de 1 ou 2 passos na direção do ponto 2) ela vai se pôr um pouco depois do Sol. Assim, logo que o Sol se põe vemos a Lua bem próximo do horizonte oeste, mas como ela está quase na mesma direção do Sol, vemos apenas uma estreita borda iluminada (que lembra uma banana). Nesta situação já devemos dizer que a Lua está no seu período crescente ou se preferirem: fase (= aparência) crescente, conforme define Mourão (1987) em seu Dicionário Enciclopédico de Astronomia e Astronáutica. A reflexão da luz da lâmpada sobre a bola de isopor imita muito bem o que se vê no céu, mas só para o(s) aluno(s) que representa(m) a Terra. Os outros alunos vêem situações completamente diferentes dependendo de onde estejam, por isso é muito importante repetir a atividade com todos os alunos (em grupos) ocupando o lugar da Terra.
- Lua quarto crescente:
Na medida em que o aluno que segura a bola de isopor se desloca para o ponto 2, vai se vendo uma porção maior da Lua iluminada, pois afinal, estamos na fase crescente. Quando a Lua chega na posição 2, os alunos que representam a Terra verão exatamente um quarto da superfície da Lua iluminada, por isso essa noite em especial, a Lua é chamada de Lua do quarto crescente. Na noite seguinte ela já não tem mais a mesma aparência, por isso não devemos mais chamá-la de quarto crescente, pois afinal, mais que um quarto de sua superfície é visível. Entretanto, ela continua no seu período crescente ou fase crescente.
- Lua cheia:
É o nome dado à Lua quando ela está na posição 3. Conforme definido anteriormente ela está passando acima da linha Terra-Sol. Todo o disco iluminado é visível da Terra. Note também que o Sol se pôs a oeste e a Lua está “nascendo” a leste, portanto a Terra está entre ambos. A Lua cheia parece maior quando está nascendo do que quando está sobre nossas cabeças, mas isso é um ilusão: basta olhá-la por um tubo estreito ou por um simples buraquinho através da nossa mão quando a fechamos, de modo a não vermos o relevo do horizonte, que veremos a Lua do mesmo tamanho que quando ela passa sobre nossas cabeças. Com a Lua cheia termina a fase crescente Na noite seguinte a Lua já não é mais cheia e começa, então, o período ou fase da lua minguante.
- Lua quarto minguante:
Cerca de sete noites após a lua cheia veremos novamente um quarto da superfície da Lua iluminada, por isso essa noite, em particular, é chamada de Lua quarto minguante, quando então ela estará passando pelo ponto 4. Note que as noites seguintes não devem ser chamadas de Lua quarto minguante, pois a palavra “quarto” se refere a um quarto da superfície iluminada e visível da Terra, o que ocorre só em duas noites particulares, sendo uma na fase crescente e outra na fase minguante.
Muitas pessoas respondem prontamente a esta questão: “não gira”! E dizem mais: “pois sempre vemos a mesma face na qual está o “São Jorge””. Nessa montagem é fácil demonstrar que a Lua gira sobre ela mesma. O aluno que segura o Sol começou esta atividade não vendo o “São Jorge”, quando a Lua estava na posição 1, pois o quadrado negro, que está representando o “São Jorge” estava voltado para a Terra. Mas quando a lua estava na posição 3, o aluno que segura a lâmpada viu o “São Jorge”; logo a Lua girou sobre ela mesma, senão isso não seria possível. Todos os outros alunos que estiverem observando a atividade confirmarão o que disse o aluno Sol, pois eles também verão as duas faces da Lua.
Claro que o aluno Terra não está muito convencido que a Lua gira sobre ela, afinal ele sempre vê o “São Jorge”. Podemos convencê-lo que a Lua gira sobre si, refazendo a demonstração mas com a Lua, de fato, não girando sobre ela. Então, começando com a Lua na posição 1 com o “São Jorge” virado para a Terra e, portanto, virado também para a posição 3 e virado, digamos, para a parede que está atrás da posição 3. O aluno que transporta a Lua, deve, então, fazer a Lua girar ao redor da Terra, mas com o “São Jorge” sempre voltado para a mesma parede que está atrás da posição 3. Feito isso, o Aluno Sol e todos aqueles que estavam ao lado dele sempre observam a mesma face da Lua e garantem que ela não girou. O aluno Terra, por outro lado, acredita que a Lua não girou sobre ela mas agora ele viu as duas faces da Lua, ou seja, agora que ficou evidente que a Lua não girou, ele viu as duas faces. Porém, isso não é a realidade. Então, a Lua realmente gira sobre ela. Esta atividade convence a muitos que a Lua gira sobre si mesma enquanto gira ao redor da Terra, mas não convence a todos. De fato, o movimento de rotação da Lua ocorre no mesmo tempo em que ela gira ao redor da Terra. Por isso vemos sempre a mesma face, isto é, o mesmo “São Jorge”.
Antes de falar em eclipse é preciso definir e entender o que é sombra e penumbra. Usando a lâmpada com o tubo de papel alumínio, projete a sombra da bola de isopor na parede. Pode-se ver que há duas regiões distintas de sombra: uma bem escura, no centro, chamada de sombra e ao redor desta, uma região menos escura chamada penumbra, conforme ilustra a Fig. 25.
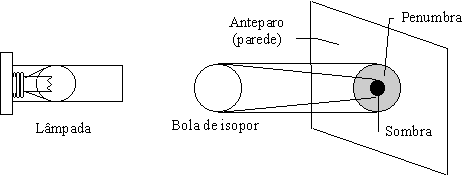
Fig.25- Esquema para visualizar a sombra e a penumbra da bola de isopor projetada sobre a parede.
Encostando a bola de isopor na parede vê-se apenas a sombra e afastando-se a bola da parede, começa a diminuir o tamanho da sombra e aumentar o tamanho da penumbra. A Terra também projeta uma sombra e uma penumbra. Quando a Lua atravessa apenas a região da penumbra da Terra dizemos que é um eclipse lunar penumbral, e quando a Lua também atravessa a sombra da Terra, temos o eclipse lunar propriamente, sendo que no penumbral a Lua continua visível, porém escurecida e no lunar ela fica invisível. Em ambos os casos pode-se ter eclipse parcial ou total da Lua. Claro que se a Lua está atravessando a sombra (ou penumbra) da Terra, a Lua está ou na lua cheia ou muito próxima dela (antes ou depois).
O eclipse solar pode ser parcial, total ou anular (quando a Lua passa exatamente na frente do Sol, mas por estar mais distante da Terra do que em outras circunstâncias não conseguiu cobrir o disco solar completamente). Se a Lua está entre a Terra e o Sol é porque é uma lua nova.
O experimento com a bola de isopor não permite ver os eclipses em todas as suas particularidades devido às desproporções entre os volumes da bola de isopor, da Terra e desproporções entre as distâncias Terra-Lua e Terra-Sol. Contudo permite simular suas ocorrências, tanto os lunares quanto os solares.
No item 4, Fases da Lua, a Terra não tinha translação. A Lua passava pela posição 1 (Fig. 24) abaixo do plano da órbita da Terra (definido como o plano paralelo ao chão e passando pelo centro da cabeça do aluno Terra), cruzava o plano da órbita da Terra na posição 2 (Fig. 24), passava pela posição 3 (Fig.24) acima do plano da órbita da Terra, passava pela posição 4 (Fig. 24) cruzando de novo o plano da órbita da Terra e recomeçava o ciclo pela posição 1 abaixo da órbita da Terra.
O plano de translação da Lua ao redor da Terra não muda enquanto esta gira ao redor do Sol. Para simular os eclipses o aluno Terra descrito no item 4, agora deverá transladar lentamente ao redor do Sol, que continuará apontando seu feixe de luz para a Lua. Na Fig.26 esquematizamos essa atividade. Conforme explicado no item 4, Fases da Lua, a inclinação entre os planos das órbitas da Lua ao redor da Terra e desta ao redor do Sol é de 5o, o que evita os dois eclipses mensais.
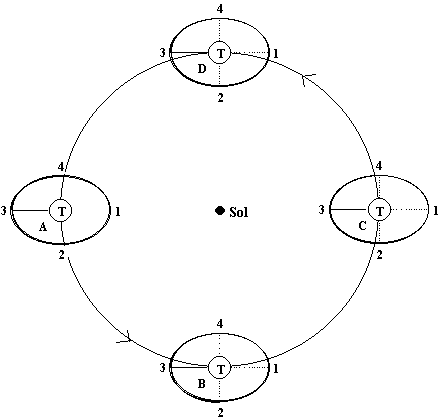
Fig. 26 - Esquema da Terra girando ao redor do sol e da Lua girando ao redor da terra em posições A, B, C, e D. Obs: A órbita da Lua não é fechada como desenhada. O desenho atende a outros propósitos explicados no texto. A linha 2-4 sempre pertence aos dois planos (órbita da Lua ao redor da Terra e órbita da Terra ao redor do Sol) simultaneamente. O ponto 1 sempre está abaixo do plano da órbita da Terra e o ponto 3 sempre acima do mesmo plano. A região pontilhada da órbita da Lua, mostra a parte da órbita que está abaixo do plano da órbita da Terra e a parte contínua da órbita da Lua mostra a parte da órbita que está acima do plano da órbita da Terra.
Toda a explicação das fases da Lua ocorreu com a Terra no ponto A da Fig 26. Note que nesta Fig. 26 o ponto 1 (semi-círculo tracejado entre os pontos 4, 1 e 2) sempre está abaixo do plano da órbita da Terra e o ponto 3 está acima do mesmo, enquanto que o segmento que liga os pontos 2 e 4 sempre pertencem a ambos os planos da órbita da Lua e da Terra, ou seja, a órbita da Lua não muda com a translação da Terra. Note que nas posições A e C nunca ocorrem eclipses, contudo nas posições B e D eles podem ocorrer, pois a Lua pode estar passando pelas posições 4 ou 2 e, portanto, cruzando a linha Terra-Sol. Quando a Lua passar pelas posições B4 ou D2 é Lua nova e um eclipse solar pode ocorrer, quando ela passar por B2 ou D4 é Lua cheia e eclipses lunares podem ocorrer. O aluno que transporta a Lua (bola de isopor) deve procurar manter sempre a mesma trajetória para a bola de isopor, independente do movimento da Terra.
Com as atividades aqui propostas, usando sempre a participação ativa dos alunos, materiais de baixo custo e disponíveis com facilidade no comércio, oferecemos ao professor de primeiro grau uma alternativa para fazer o ensino dos conceitos básicos de astronomia de uma forma mais realista, correta e motivadora para o aluno.
Beltrame, Z. V., Geografia Ativa - Investigando o Ambiente do Homem, vol. 1, 1996, Ed. Ática.
Bizzo, N., et al, Graves erros de conceito em livros didáticos de ciências, Ciência Hoje, no 121, (21), 26 - 35, 1996.
Canalle, J.B.G., Trevisan, R.H. e Lattari, C.J.B., Análise do conteúdo de astronomia dos livros de geografia de 1o grau, Cad. Cat. Ens. Fís., v. 14, no 3, 1997, p. 254 - 263, dez. 1997.
Mourão, R.R.F., Dicionário Enciclopédico de Astronomia e Astronáutica, 1a Ed., 1987, Editora Nova Fronteira.
Trevisan, R.H., Lattari, C.J.B. e Canalle, J.B.G., Assessoria na avaliação do conteúdo de astronomia dos livros de ciências do primeiro grau, Cad. Cat. Ens. Fís., v. 14, no 1, p. 7, 1997
Talvez um dos mais antigos instrumentos astronômicos conhecidos, o relógio de sol, ainda hoje desperta a curiosidade das pessoas, pois com apenas a sombra de seu indicador temos a marcação das horas.
Claro que hoje temos instrumentos mais precisos, que nos fornecem as mesmas informações que o Relógio de sol, mas para um primeiro contato e também para desvendar alguns pequenos segredos que envolvem o Relógio de sol, idealizamos um relógio de fácil construção, e que pode ser feito inclusive com as folhas de caderno, de cartolina ou até mesmo (para os mais habilidosos) de madeira.
Como sabemos, um relógio é composto por um indicador das horas, um ponteiro e um conjunto de engrenagens que vão fazê-lo funcionar. O Relógio de sol também é composto de um indicador das horas e um ponteiro, mas o conjunto de engrenagens será substituído pelo nosso Sol.
Passamos a descrever abaixo, como podemos montar um Relógio de sol com mostrador horizontal de horas.
Para a confecção do mostrador, utilizaremos uma folha de sulfite onde traçaremos as linhas horárias (ou as linhas que indicam as horas).
Para isso, alguns conhecimentos de trigonometria e da latitude do local (latitude onde está localizada a sua cidade) serão necessários, pois temos que calcular os ângulos que definirão as linhas horárias, os quais são obtidos com as informações acima e com a seguinte expressão :
![]()
Onde :
X = ângulo, em graus, que a linha das horas faz com a linha das doze horas, ou linha meridiana do relógio;
![]() = latitude do local;
= latitude do local;
6 < hora < 12
Como o Sol descreve aparentemente um círculo (360º) em 24 horas, temos que cada hora corresponde a 15 graus. Para hora = 6 ou 12 horas, temos tangente de 900 e 00 a qual não é definida, mas para as 6 horas da manhã a linha das horas coincide com a direção leste-oeste e para as 12 horas a linha das horas coincide com o meridiano local (linha central da base do relógio de sol.)
Para traçarmos a linha das doze horas, dobramos o papel sulfite exatamente ao meio e então traçamos a reta que passa exatamente pelo meio do papel, de um lado ao outro.
Feito isto, desenharemos um retângulo na folha com lado menor de 20 cm e lado maior de 29,5 cm, como mostra a Fig. 27. Neste ponto, devemos marcar na origem da linha das 12 horas o ponto cardeal norte e no extremo oposto o ponto cardeal sul.
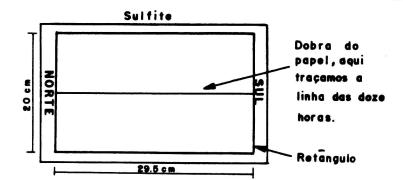
Figura 27- Linha das 12 horas
Para a determinação das linhas horárias (ou linha das horas) vamos tomar como exemplo a latitude de -22º54’, que corresponde à cidade do Rio de Janeiro.
Utilizando a expressão descrita anteriormente, chegamos a valores do ângulo X os quais podem ser vistos na tabela seguinte:
|
Linhas das horas |
Ângulo (x) (em relação às 12 horas) (em graus) |
|
12 |
0,0 |
|
11 e 13 |
5,9 |
|
10 e 14 |
12,6 |
|
09 e 15 |
21,2 |
|
08 e 16 |
33,9 |
|
07 e 17 |
55,4 |
|
06 e 18 |
90,0 |
Observação: Devemos lembrar também que os ângulos são válidos tanto para o lado esquerdo da linha das 12 horas quanto para o lado direito.
Uma das maneiras para prosseguir o trabalho a partir deste ponto é escolhermos uma origem na linha horária das 12 horas, e a partir deste ponto, marcarmos os ângulos encontrados para as linhas horárias. Feito isto, traçamos, finalmente, as linhas horárias e marcamos em seus extremos as horas correspondentes. Ver Fig. 28.
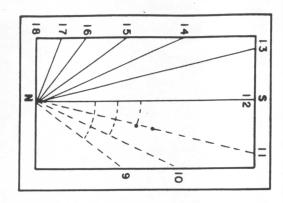
Figura 28 – Esquema da base do relógio de Sol
Para confeccionar o ponteiro, basta que numa folha de papel tracemos uma reta, a qual chamaremos de reta 1 com 20,0 cm de comprimento, e com um transferidor marcar o valor do ângulo que a latitude do local faz com essa reta, a partir de uma origem, acima e abaixo da reta como mostra a Fig. 29.Traçamos as retas (as quais indicaremos como retas 2 e 3) entre o ponto marcado do ângulo e a reta 1.
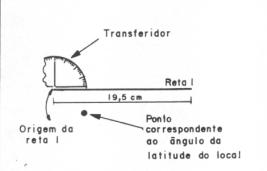
Figura 29- Determinação do ângulo correspondente à latitude local
Após esta etapa, traçamos uma reta paralela às retas 2 e 3 distantes a 1 cm das retas 2 e 3. Liga-se, então, os pontos como mostra a figura30.
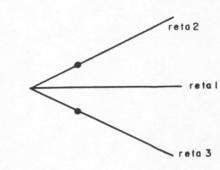
Figura 30- Esquema das retas 2 e 3 referente ao ângulo da latitude local
Estando prontas as marcações do ponteiro, recortamos e dobramos como mostra a Figura 31.
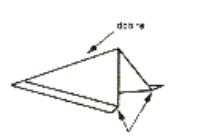
Figura 31- Indicação de como dobrar o ponteiro
Estando dobrado o ponteiro, colamos a parte de dentro do ponteiro, e após isto colamos o mesmo com sua parte mais baixa (ponta) coincidindo com a marcação do norte do relógio exatamente por cima e ao longo das doze horas, como ilustra a Fig. 32.
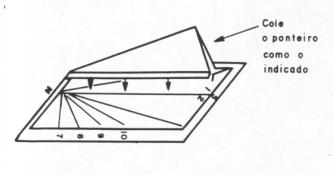
Figura 32- Indicação de como colar o ponteiro sobre a base do relógio de sol
As marcações dos pontos norte e sul, como poder-se-ia pensar a princípio que seria apenas para indicar os pontos cardeais, tem uma simples, mas importante função. Qual seria ela?
Claro! Direcionar o relógio do sol na linha norte-sul, para que possamos ter a sombra projetada do Sol no mostrador, pois como sabemos o Sol faz um movimento do leste para o oeste e, portanto se o ponteiro está perpendicular a este movimento, teremos as sombras projetadas.
Para isso, podemos utilizar três recursos práticos: 1) utilizar uma bússola e encontrar a posição norte magnética (a qual é próxima da geográfica, tendo uma diferença de mais ou menos 18 graus, e desta maneira direcionar o relógio de sol), ou 2) utilizarmos de nosso próprio relógio, para posicionarmos o relógio de sol (talvez este seja o mais fácil) e 3) fazermos uso de um gnômon.
Se fixarmos um relógio de sol num local, e observarmos ao longo dos meses, num mesmo horário, verificaremos que o relógio adianta-se, atrasa-se ou se iguala em relação ao seu relógio mecânico ou digital.
Os modernos relógios que usamos, nos informam o Tempo Legal que é uma variedade do que chamamos Tempo Médio. Este Tempo Médio é o tempo ditado pela marcha do chamado “Sol médio”, um Sol fictício ou imaginário, que faria seu caminho exatamente igual no céu dia após dia.
Como você já viu anteriormente neste curso, o Sol tem um movimento aparente que modifica sua posição com o passar dos meses fazendo, portanto, com que o nosso bom relógio de sol se atrase, se adiante ou se iguale com nossos relógios de pulso.
Ao dar a oportunidade aos alunos de confeccionar o relógio de sol, podemos além de ensinar alguns conceitos básicos de astronomia, tais como movimento aparente do Sol, Tempo Médio, etc; podemos também utilizar conceitos matemáticos de trigonometria e geometria, além de desenvolver suas habilidades manuais.